- ж¬ўиҝҺи®ҝй—®жө·еҚ—жҲҗдәәй«ҳиҖғзҪ‘пјҒ жң¬зҪ‘з«ҷдё»иҰҒдёәжө·еҚ—дё“еҚҮжң¬гҖҒй«ҳиө·жң¬гҖҒй«ҳиө·дё“жҲҗиҖғиҖғз”ҹжҸҗдҫӣжҠҘиҖғжҢҮеҜјжңҚеҠЎпјҢзҪ‘з«ҷдҝЎжҒҜд»…дҫӣеӯҰд№ дәӨжөҒдҪҝз”ЁпјҢе®ҳж–№дҝЎжҒҜд»Ҙжө·еҚ—зңҒиҖғиҜ•еұҖea.hainan.gov.cnдёәеҮҶгҖӮ
- е’ЁиҜўпјҡ15180456453








 пјҢеҲҷsin2a=
пјҢеҲҷsin2a=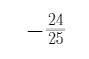



 зғӯй—Ёзӣёе…іиҜ•еҚ·
зғӯй—Ёзӣёе…іиҜ•еҚ·








